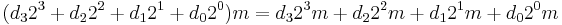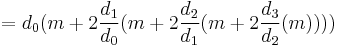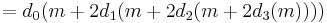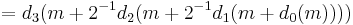Horner scheme
In numerical analysis, the Horner scheme (also known as Horner algorithm), named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation. The Horner scheme can also be viewed as a fast algorithm for dividing a polynomial by a linear polynomial with Ruffini's rule.
Contents |
Description of the algorithm
Given the polynomial
where  are real numbers, we wish to evaluate the polynomial at a specific value of x, say x0.
are real numbers, we wish to evaluate the polynomial at a specific value of x, say x0.
To accomplish this, we define a new sequence of constants as follows:
Then b0 is the value of p(x0).
To see why this works, note that the polynomial can be written in the form
Thus, by iteratively substituting the 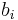 into the expression,
into the expression,
Examples
Evaluate
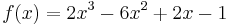 for
for 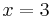 .
.
We use synthetic division as follows:
x₀│ x³ x² x¹ x⁰
3 │ 2 -6 2 -1
│ 6 0 6
└────────────────────────
2 0 2 5
The entries in the third row are the sum of those in the first two. Each entry in the second row is the product of the x-value (3 in this example) with the third-row entry immediately to the left. The entries in the first row are the coefficients of the polynomial to be evaluated. Then the remainder of  on division by
on division by 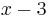 is 5.
is 5.
But by the remainder theorem, we know that the remainder is 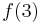 . Thus
. Thus 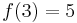
In this example, if 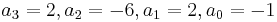 we can see that
we can see that 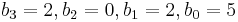 , the entries in the third row. So, synthetic division is based on Horner Scheme.
, the entries in the third row. So, synthetic division is based on Horner Scheme.
As a consequence of the polynomial remainder theorem, the entries in the third row are the coefficients of the second-degree polynomial, the quotient of  on division by
on division by 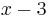 . The remainder is 5. This makes Horner's method useful for polynomial long division.
. The remainder is 5. This makes Horner's method useful for polynomial long division.
Divide 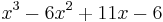 by
by 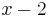 :
:
2 │ 1 -6 11 -6
│ 2 -8 6
└────────────────────────
1 -4 3 0
The quotient is 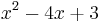 .
.
Let 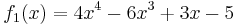 and
and 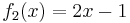 . Divide
. Divide 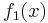 by
by 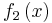 using Horner's scheme.
using Horner's scheme.
2 │ 4 -6 0 3 │ -5
────┼──────────────────────┼───────
1 │ 2 -2 -1 │ 1
│ │
└──────────────────────┼───────
2 -2 -1 1 │ -4
The third row is the sum of the first two rows, divided by 2. Each entry in the second row is the product of 1 with the third-row entry to the left. The answer is
Floating point multiplication and division
Horner's method is a fast, code-efficient method for multiplication and division of binary numbers on a microcontroller with no hardware multiplier. One of the binary numbers to be multiplied is represented as a trivial polynomial, where, (using the above notation): ai = 1, and x = 2. Then, x (or x to some power) is repeatedly factored out. In this binary numeral system (base 2), x = 2, so powers of 2 are repeatedly factored out.
Example
For example, to find the product of two numbers, (0.15625) and m:
Method
To find the product of two binary numbers, "d" and "m".
- 1. A register holding the intermediate result is initialized to (d).
- 2. Begin in (m) with the least significant (rightmost) non-zero bit,
- 2b. Count (to the left) the number of bit positions to the next most significant non-zero bit. If there are no more-significant bits, then take the value of the current bit position.
- 2c. Using that value, perform a right-shift operation by that number of bits on the register holding the intermediate result
- 3. If all the non-zero bits were counted, then the intermediate result register now holds the final result. Otherwise, add (d) to the intermediate result, and continue in step #2 with the next most significant bit in (m).
Derivation
In general, for a binary number with bit values: (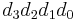 ) the product is:
) the product is:
At this stage in the algorithm, it is required that terms with zero-valued coefficients are dropped, so that only binary coefficients equal to one are counted, thus the problem of multiplication or division by zero is not an issue, despite this implication in the factored equation:
The denominators all equal one (or the term is absent), so this reduces to:
or equivalently (as consistent with the "method" described above):
In binary (base 2) math, multiplication by a power of 2 is merely a register shift operation. Thus, multiplying by 2 is calculated in base-2 by an arithmetic shift. The factor (2−1) is a right arithmetic shift, a (0) results in no operation (since 20 = 1, is the multiplicative identity element), and a (21) results in a left arithmetic shift. The multiplication product can now be quickly calculated using only arithmetic shift operations, addition and subtraction.
The method is particularly fast on processors supporting a single-instruction shift-and-addition-accumulate. Compared to a C floating-point library, Horner's method sacrifices some accuracy, however it is nominally 13 times faster (16 times faster when the "canonical signed digit" (CSD) form is used), and uses only 20% of the code space.[1]
Polynomial root finding
Using the Horner scheme in combination with Newton's zero finding method it is possible to approximate the real roots of a polynomial. The algorithm is as follows. Given a polynomial 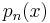 of degree
of degree  with zeros
with zeros 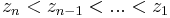 make some initial guess
make some initial guess 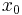 such that
such that 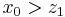 . Now follow the steps outline below.
. Now follow the steps outline below.
1. Using Newton's method find the largest zero, 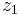 of
of 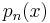 using the guess
using the guess 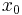 .
.
2. Use the Horner scheme to divide out 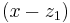 to obtain
to obtain 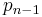 . Return to step 1 but use the polynomial
. Return to step 1 but use the polynomial 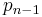 and the initial guess
and the initial guess 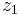 .
.
These two steps are repeated until all real zeros are found for the polynomial. If the approximated zeros are not precise enough, the obtained values can be used as initial guesses for Newton's method but using the full polynomial rather than the reduced polynomials.[2]
Example
Consider the polynomial,
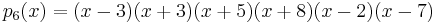
which can be expanded to,
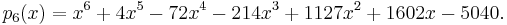
From the above we know that the largest root of this polynomial is 7 so we are able to make an initial guess of 8. Using Newton's method the first zero of 7 is found as shown in black in the figure to the right. Next 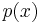 is divided by
is divided by 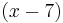 to obtain,
to obtain,
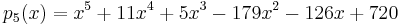
which is drawn in red in the figure to the right. Newton's method is used to find the largest zero of this polynomial with an initial guess of 7. The largest zero of this polynomial which corresponds to the second largest zero of the original polynomial is found at 3 and is circled in red. The degree 5 polynomial is now divided by 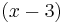 to obtain,
to obtain,
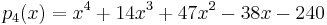
which is shown in yellow. The zero for this polynomial is found at 2 again using Newton's method and is circled in yellow. The Horner scheme is now used to obtain,
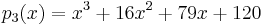
which is shown in green and found to have a zero at -3. This polynomial is further reduced to,
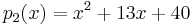
which is shown in blue and yields a zero of -5. The final root of the original polynomial may be found by either using the final zero as an initial guess for Newton's method, or by reducing 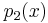 and solving the linear equation. As can be seen, the expected roots of -8, -5, -3, 2, 3, and 7 were found.
and solving the linear equation. As can be seen, the expected roots of -8, -5, -3, 2, 3, and 7 were found.
Octave implementation
The following Octave code was used in the example above to implement the Horner scheme.
function [y b] = horner(a,x) % Input a is the polynomial coefficient vector, x the value to be evaluated at. % The output y is the evaluated polynomial and b the divided coefficient vector. b(1) = a(1); for i = 2:length(a) b(i) = a(i)+x*b(i-1); end y = b(length(a)); b = b(1:length(b)-1); end
Python implementation
The following Python code implements the Horner scheme.
def horner(x, *args): """A function that implements the Horner Scheme for evaluating a polynomial of coefficients *args in x.""" result = 0 for coefficient in args: result = result * x + coefficient return result
Application
The Horner scheme is often used to convert between different positional numeral systems – in which case x is the base of the number system, and the ai coefficients are the digits of the base-x representation of a given number – and can also be used if x is a matrix, in which case the gain in computational efficiency is even greater. In fact, when x is a matrix, further acceleration is possible which exploits the structure of matrix multiplication, and only 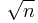 instead of n multiplies are needed (at the expense of requiring more storage) using the 1973 method of Paterson and Stockmeyer[3].
instead of n multiplies are needed (at the expense of requiring more storage) using the 1973 method of Paterson and Stockmeyer[3].
Efficiency
Evaluation using the monomial form of a degree-n polynomial requires at most n additions and (n2 + n)/2 multiplications, if powers are calculated by repeated multiplication and each monomial is evaluated individually. (This can be reduced to n additions and 2n - 1 multiplications by evaluating the powers of x iteratively.) If numerical data are represented in terms of digits (or bits), then the naive algorithm also entails storing approximately 2n times the number of bits of x (the evaluated polynomial has approximate magnitude xn, and one must also store xn itself). By contrast, Horner's scheme requires only n additions and n multiplications, and its storage requirements are only n times the number of bits of x. Alternatively, Horner's scheme can be computed with n fused multiply–adds. Horner's scheme can also be extended to evaluate the first k derivatives of the polynomial with kn additions and multiplications.[4]
It has been shown that the Horner scheme is optimal, in the sense that any algorithm to evaluate an arbitrary polynomial must use at least as many operations. That the number of additions required is minimal was shown by Alexander Ostrowski in 1954; that the number of multiplications is minimal by Victor Pan, in 1966. When x is a matrix, the Horner scheme is not optimal.
This assumes that the polynomial is evaluated in monomial form and no preconditioning of the representation is allowed, which makes sense if the polynomial is evaluated only once. However, if preconditioning is allowed and the polynomial is to be evaluated many times, then faster algorithms are possible. They involve a transformation of the representation of the polynomial. In general, a degree-n polynomial can be evaluated using only 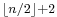 multiplications and n additions (see Knuth: The Art of Computer Programming, Vol.2).
multiplications and n additions (see Knuth: The Art of Computer Programming, Vol.2).
History
Even though the algorithm is named after William George Horner, who described it in 1819, the method was already known to Isaac Newton in 1669, the Chinese mathematician Qin Jiushao in his Mathematical Treatise in Nine Sections in the 13th century, and even earlier to the 11th century Song dynasty mathematician Jia Xian, and the Persian Muslim mathematician Sharaf al-Dīn al-Tūsī in the 12th century.[6] The earliest use of Horner's scheme was in The Nine Chapters on the Mathematical Art, a Chinese work of the Han Dynasty (202 BC – 220 AD) edited by Liu Hui (fl. 3rd century).[7]
See also
- Clenshaw algorithm to evaluate polynomials in Chebyshev form
- De Casteljau's algorithm to evaluate polynomials in Bézier form
- De Boor's algorithm to evaluate splines in B-spline form
- Estrin's scheme that is amenable to parallelization on modern computer architectures.
References
- ^ Kripasagar, March 2008, "Efficient Micro Mathematics", Circuit Cellar, p.62, issue 212
- ^ Kress, Rainer, "Numerical Analysis", Springer, 1991, p.112,
- ^ Higham, Nicholas. (2002). Accuracy and Stability of Numerical Algorithms. Philadelphia: SIAM. ISBN 0898715210. Section 5.4.
- ^ W. Pankiewicz. "Algorithm 337: calculation of a polynomial and its derivative values by Horner scheme". http://portal.acm.org/citation.cfm?doid=364063.364089.
- ^ Urich Librecht Chinese Mathematics in the Thirteenth Century, p181-191, Dover ISBN 0-486-44619-0
- ^ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), p. 304–309.
- ^ Temple, Robert. (1986). The Genius of China: 3,000 Years of Science, Discovery, and Invention. With a forward by Joseph Needham. New York: Simon and Schuster, Inc. ISBN 0671620282. Page 142.
Bibliography
- William George Horner. A new method of solving numerical equations of all orders, by continuous approximation. In Philosophical Transactions of the Royal Society of London, pp. 308–335, July 1819.
- Spiegel, Murray R. (1956). Schaum's Outline of Theory and Problems of College Algebra. McGraw-Hill Book Company.
- Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Pages 486–488 in section 4.6.4.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Problem 2-3 (pg. 39) and page 823 of section 30.1: Representation of polynomials.
- Kripasagar, Venkat (March 2008). "Efficient Micro Mathematics – Multiplication and Division Techniques for MCUs". Circuit Cellar magazine (212): p. 60.
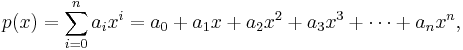
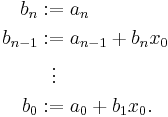
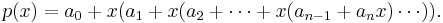
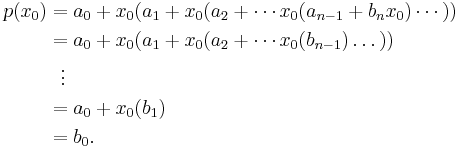
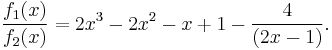
![\begin{align}
( 0.15625) m & = (0.00101_b) m = ( 2^{-3} %2B 2^{-5}) m = (2^{-3})m %2B (2^{-5})m \\[4pt]
& = 2^{-3} (m %2B (2^{-2})m) = 2^{-3} (m %2B 2^{-2} (m)).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/51b312a929ec87780ce57bd9762f2066.png)